Institute for Christian Teaching
Education Department of
Seventh-day Adventists
GOD IN NATURE:
REVELATIONS OF THE
DIVINE MATHEMATICIAN
by
Avery J. Thompson
Associate Professor of
Mathematics
West Indies College
Prepared for the
Faith and Learning Seminar
held at
West Indies College
Mandeville, Jamaica - June
16-28, 1996
269-96
Institute for Christian Teaching
12501
Old Columbia Pike
Silver
Spring, MD 20904 USA
INTRODUCTION
In presenting this paper I
have assumed that, as Christian educators, we have a Christ-centered worldview
and as such clearly see the need for the integration of faith and learning in
the classroom.
When we teach students mathematics, it is expected
that they will develop; an awareness of the order, logic and precision that are
characteristic of the Creator; a growing knowledge of God's faithfulness and dependability;
and the skills of logical thinking and presentation. We also find it essential
to instill in them an awareness of consequences, potential, balance, caution,
choice, learning from mistakes, order, awe, informed decision making, logic,
following instructions, adherence to principles, sharing, stewardship,
appreciation of the Master Designer, reasoning processes, discipline,
perceptiveness, creativity, dependability, and personal responsibility. (Hill,
1990)
However, many teachers of mathematics find it challenging to properly
integrate faith and learning in their classroom. The method of parallelism is
the one most often employed by those who realize the need to portray values in
their delivery.
This paper presents a
mathematical model of creation,
deterioration and restoration as
a starting point for the teacher. Throughout, mathematical applications have
been used to help illustrate the processes by which God makes Himself known to
us--His principles, His judgments, His all-sustaining power and His constant
connection to help better mankind. Students as well as teachers are involved in
the natural processes of creation and as such should be able to relate to the
examples presented.
If properly approached, the study of nature may...penetrate the devastating
problem of sin and God's redeeming grace and...lead to a clearer understanding
of the laws and operations of nature, the laws that operates in human life and
the great principles of truth that govern the spiritual universe. (Taylor, 2CC)
Recently, students of mine,
in Precalculus I, were given a group project in which they were required to
show evidences of mathematics in nature. They were to present in pictorial or
graphical format, ten (10) examples. If the picture or graph was not self-explanatory,
then they would have one paragraph to explain what concept they were
presenting. Out of those projects, I have chosen several to present in this
paper to show how these students gained insight into a orderly, logical, caring
and loving Father/Creator. (Teacher
explanations are provided in the appendix - page 13ff)
THE BASE
In working problems in
mathematics students are often faced with the dilemma of not knowing what to do
first. To many the saying, "Fools rush in where angels fear to tread"
(anon) becomes a personal reality. One of the most famous mathematicians of
this century was George Polya, late Professor of Mathematics at Stanford
University. His discoveries have included the areas of real and complex
analysis, probability, combinatorics, number theory and geometry. His
publications exude such clarity and elegance that they are a joy to read.
(Smith, 1987)
Polya in 1945, developed a
model for problem solving which he later published in his book How to Solve It. This classic points out
four main steps to use; Understand the
problem, Devise a plan, Carry out the plan, Look back (examine the solution
obtained). To complete this book of mathematical strategies, Polya includes
many problems worked out with his basic four-step model as well as history and
good advice. Modern day mathematicians
still find this book indispensable.
God the Creator, a Mathematician, who impressed Polya to
"discover" these procedures that would help humans in their reasoning
and implementation of mathematical principles, had been applying them before
Polya was born. The crucial difference between the man who presented us with
this approach and an omniscient God is that the Divine Mathematician knows the
problems that will occur and has already devised plans to solve them.
CREATION
Evidences of
Order and Structure
"The earth was without form and void; and
darkness was on the face of the deep" (Gen 1:2) clearly indicated that
there was a problem to be solved. In looking at the work of the Creator, we
observe a carefully sequenced order of events used to solve this challenging
phenomenon. The devised a plan and carried out the plan. The sequence or order
of working out a problem has to be carefully thought out and analyzed before
conclusions can be drawn. Each part of
a problem depends on the "conclusion" or "creation" of the
previous step. You must know the first
term, the last term and the difference between each term in order to obtain a
desired arithmetic sequence. Follow the sequence that was implemented to answer
the barrenness of earth.
Sequencing - On day one, day and night were brought into being; on day two, the
firmament; on day three, the earth and seas, grass, plants bearing seed and
trees bearing fruit. On the fourth day, the creation of sun, moon and stars took
place; on the fifth day, the fish and birds. On the sixth day, He created the
cattle, creeping things, beasts of the earth and man and woman. On the seventh day, the Creator rested--thus
setting an example for us of cyclic behaviors. (Gen 1:3 - Gen 2:3)
Each successive day's creation depended on what had
been done before. It would have been a chaotic condition if the fish were
created before the waters were separated, or man created before the dry land
was put in place.
Categorization - God divided His creation into categories--the fish, the birds, the
firmament, the light, the beasts, man and woman. These divisions that may have
seemed haphazard made it remarkably easy for Noah to execute the command from
God to have the animals enter the ark, in pairs, each after its kind (Gen
6:19,20). The distinction had been laid out from the beginning.
Shape and form - The shape and form of each animal, plant, being, was to fit them for
the role they were to play in occupying, enjoying, nurturing and replenishing
the earth. Some were made to creep, some to walk on all fours or eights, some
to fly, some to swim, others to hop, and man was made to walk on two feet. The
form of each creature lent itself to its mode of transportation, reproduction,
identification, survival and overall well-being on the earth. Each was in tune
with the other and helped to make the quality of life perfect.
Mathematical
Exactitudes
CONSTANCY
"Kind" - Being constant implies remaining the same; never changing; keeping
the same value--a principle established from creation by a God who also placed
in man the desire to "consolidate the bewildering variety presented by his
environment into an orderly pattern." Man has "the urge to classify,
to create order from disorder, and on this to base ideas and conclusions of a
general nature..." (Guyer & Lane, 1964)
Sexuality/gender - It began in the Garden of Eden when the methodical God of systems
and patterns instilled in Adam the ability to identify the various categories
of plants, birds, sea creatures, et cetera and thus he named each creature. He
gave names to the cattle, to the birds and to the beasts and to his mate (Gen
2:20). It is not clear what criteria Adam used in naming these other occupants
of Eden but he declared "This is now hone of my bones and flesh of my
flesh; She shall be called Woman, because she was taken out of Man' to clearly
define that he recognized his counterpart.
The species placed on this earth by the Creator still exhibit the
general characteristics with which they were created. Regardless of the
movement to occupy the earth, human beings still have the same basic form.
Though the offsprings of creation may differ in color, in height, in build, in
size--a man is still a man and a woman is still a woman; birds still fly, fish
still swim, insects crawl and/or fly, beasts of the field still graze, etc.
Though each specie may have had to adapt to its environment, they continue to
reproduce and each successive generation exhibits similar attributes to that of
their predecessors.
Axis & Balance - Division of the body in half, length-wise, show that man/woman is in
balance (for the most part) on both sides of his/her body. If this line of
demarcation is looked at as the y-axis, it can be seen that man/woman was
created in perfect bilateral symmetry.
That is, the line would represent a mirror from which the image was the
same distance as the reflection in it.

This principle also applies to the rest of creation.
In some instances, the reflection
phenomena is much more extensive and can therefore be viewed as being symmetric
to the origin, as in the case of a starfish. {If the center of the starfish is
established, then any point or appendage has
its match on the opposite side, and a straight line, though the origin, can
be used to connect them.}
PRECISION
Ecological Balance - Balance must be
maintained between two sides of an equation. Addition or subtraction of a
variable on one side of the equation, has its correlation on the other side.
Each element of creation contributes to the ecological balance that enables
life as we know it, to continue. While man continues in his quest to make a
"perfect" world, he still requires other organisms in his
environment, in order to maintain balance (equality) and thus ensure his
existence and general continuity.

Environmental Effects - The tilt of the earth, a
precise angle of refraction, provides for the temperature differences on the
earth, the undulating of tides, the patterns of rain, the seasonal changes....
The earth in its orbit around the sun keeps the planet at temperatures that
will sustain us.
If moved
out of our orbit, or shifted at a greater angle, life could not be the same.
Destruction to our earth and its life would be caused by either increasing the
temperature too much (if moved closer to the sun) or lowering it too much (if
moved further from the sun). The gravitational pull on the earth has allowed us
to unfold laws of physics, based on mathematical principles.
Subsets of
Life Forms
There is a universal set of
God's implementation that has as subsets, the various life forms. On the
periphery, there exist viruses and bacteria.
Then we have the species of
plants...then animals and finally man. Each of these exists only with the
influence of the others. Man who was made "a little lower than the
angels" (Heb 2:7) is still dependent on all other life-forms for his
existence.
When all was done, before
resting on the Sabbath, God implemented the last step, pointed out by Polya, to
determine the validity of the conclusion drawn. He looked back and "saw
everything that He had made, and indeed it was very good." (Gen 1:31)
"Everything was perfect in its kind; every creature met the goal appointed
by the Creator, and was equipped to accomplish the purpose for which it was
created." (SDA Bible Commentary, Vol. 1).
DETERIORATION
Deception by
Exclusion
Invalid Assumption - A new "problem"
presents itself to the Great Mathematician. Sin enters the world and
deterioration of all perfection has begun. According to the rules of logic, the
only equivalent and/or valid form of a statement is its contrapositive--not its
negation. God said "You shall not eat it, nor shall you touch it, lest you
die" (Gen 2:17). The Statement
"You will not surely die" (Gen 3:4), made by the serpent, is not
equivalent in meaning. It led to an invalid conclusion/assumption, that is, the
negation of the original statement.
Progressive Degeneration - The concepts of permutations are prescribed in
mathematics to help in the calculation of the number of events possible in a
predescribed situation. The rapid growth of sin took on a momentum that can be
likened to an expression whose result approaches infinity.

Adam and Eve ate the forbidden fruit and started the
chain reaction. Cain, their son murdered his brother. Cain's great-great-great
grandson also murdered a young man though he claimed that it was in
self-defense. (Gen 4:8-24)
Distortion of
Shapes and Forms
Though life forms display
characteristics close to those with which they were created, the degenerative
effects can be likened to the observations seen in similar triangles. The
corresponding angles and sides of each bear the same proportional relationship,
but the triangles may be of different sizes. If one compares the height of Adam
to present day man, the proportion of approximately 18ft to 6ft is a 3:1 ratio.
"As Adam came forth from the hand of his Creator, he was of noble height,
and of beautiful symmetry. He was more than twice as tall as men now living
upon the earth, and was well proportioned." (White, 1945)
If Adam were twelve feet tall or more, he could have weighed nearly a
ton. An increase in height of more than two times would increase the weight by
more than eight times, because there would be a corresponding increase in
girth, as well as height, in order to maintain the same proportions. Adam was a
giant....(Coffin, 1969)
"If Adam, at his
creation, had not been endowed with twenty times as much vital force as men now
have, the race, with their present habits of living...would have become extinct."
(White, 1948)
Mankind, who named all
created beings, built a tower that was to reach the heavens, used triangulation
to mortally would their enemies and constructed the great pyramids, is today
reputed by scientists to use only between five and ten percent of their brain
capacity.
Most of the patriarchs from Adam to Noah lived
nearly a thousand years and yet since the days of Noah, mankind lives an
average of 70 years. Larger animals help to keep the balance of nature by
preying on smaller species. Different species have become extinct due to
predators, harsh environmental conditions (supernatural or otherwise) or
genetic degeneration. All life and capacities move towards diminution. The
ratios shows increased disparity as life continues. Ellen White (1968) declares:
The God of nature is perpetually at work. His infinite power works
unseen, but manifestations appear in the effects which the work produces. The
same God who guides the planets works in the fruit orchard and in the
vegetables garden. He never made a thorn, a thistle, or a tare. These are
Satan's work, the result of degeneration, introduced by him among the precious
things; but it is through God's immediate agency that every bud bursts into
blossom.
Deviation from Point of Contact - Velocities add as vectors. That is, the tail
of one is connected to the head of another and the resultant taken. When man is
sinned, (moved away from his original designation), it was equivalent to a
pilot plotting a course, but forgetting that the direction of the wind can
place one in a different location than one charted using only speed of the
craft and direction desired.
The things of nature that we now behold give us but a faint conception
of Eden's glory. Sin has marred earth's beauty; on all things may be seen
traces of the work of evil. Yet much that is a beautiful remains. Nature
testifies that One infinite in power, great in goodness, mercy and love,
created the earth, and filled it with life and gladness. Even in their blighted
state, all things reveal the handiwork of the great Master Artist. Wherever we
turn we may hear the voice of God and see evidences of His goodness. (White,
1964)
Though man seems to have
forgotten his Creator many times, God was still intervening in the affairs of
man and sought to bring him back to his original purpose.
RESTORATION
The Divine Focal Point
Before man sinned, God knew
his heart and devised a plan for his redemption. Now He carries out the
plan--the plan of restoration.
Mathematicians employ the
implication sign when they want to stress why some conclusion can be drawn.
God, in His infinite wisdom, didn't imply what man would need. Rather, He gave
him a ten-step model, found in Exo 20:8 -11, to point him back to the
perfection with which he was created. The paradigm is that all are interwoven.
And Jesus, Himself, summarized them into two main responsibilities: love for
God and love for humankind. (Matt 22:37 - 40)
In linear programming, the function to be maximized
(or minimized) is called the object function. Although there are usually
infinite solutions to the system of constraints called feasible solutions, the
object is to find one solution, that gives the maximum (or minimum) value of
the object function. The system of constraints,
represented by linear inequalities, require that all variables be
nonnegative. Though there may be many
external factors and man is called upon to maximize, subject to personal
conditions, two of the inequalities of the lines bounding the feasible region
of salvation are already defined. The y
$ 0 (vertical line) depicts
the "line" defining of love for God, and the x $ 0 (horizontal line) depicts
the "line" defining love for man. If and only if (IFF) you display
love for God and your fellow man (with all its implications), will your optimum
solution be found in the feasible region. (Haeussler & Paul, 1993)
In the book Counsels to Teachers, E. White states
that "...a better than earthly reward awaits those who, basing their work
on the solid Rock, build up symmetrical characters, in accordance with the
living word.
Based on the axioms,
postulates, theorems and previously acquired knowledge, inherent in the study
of mathematics, mathematicians can utilize several different routes to solve
any given problem. No matter what method
is employed, as long as mathematical integrity is maintained, the resultant
will be the same. When God put the plan of salvation in place, it was a single
imperative. "Nor is there salvation in any other, for there is no other
name under heaven given among men by which we must be saved" (Acts 4:12)
All have access to it and may adhere to it through different routes and/or
avenues, but the plan has meaning only as it is accepted.
Christ died to redeem
humankind and thus provide for them the way back to perfection. When the heart
and mind are attuned to the love, care and redemptive outreach of God, man will
once again, be a reflection of His glory.
CONCLUSION
Any credence given to the
study of mathematics must recognize that God is the original mathematician. And
though, through the ages, humankind has experimented to be able to draw
conclusion in the areas of mathematics, God's laws are error-free and
constant. His everlasting watch-care in the "natural" cyclic
phenomena of this earth daily prove His
mathematical supremacy. Galileo is remembered for having acknowledged that
"mathematics is the language that God used to create the universe."
The December 1993/January
1994 edition of The Journal of Adventist
Education makes a profound statement:
Everywhere in nature are evidences of mathematical relationships. These
are shown in ideas of number, form, design, and symmetry, and in the laws
governing the existence and harmonious working of all things. [In] the study of
these laws, ideas, and processes, mathematics reveals some of God's creative
attributes. Learning mathematical processes, axioms, and laws can help students
to more clearly identify God's design and handiwork in nature. These show Him
to be a God of system, order, and accuracy who can be depended upon. His logic
is certain. By thinking in mathematical terms, we are actually thinking God's
thoughts after Him.
When
God created the earth, everything was perfect. There was symmetry, beauty and
constancy and He was pleased with His work. However, when man, the crowning act
of God's creation sinned, deterioration commenced and the subsequent disorder
led to the defacing of God's handiwork. It is to procure the restoration of the
image of God in man, that led Christ to Calvary and the divine process will
thus have come full circle when the divine imperative is achieved.
APPENDIX
One
can see his reflection in a lake, not just his reflection, but the
reflection of the environment around him. The lake itself could be termed
an axis of symmetry or plan reflection. And if the lake is completely
undisturbed, it will reflect the environment; as if it were a flat mirror.
|
|
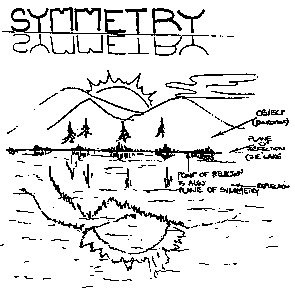
FIGURE 1
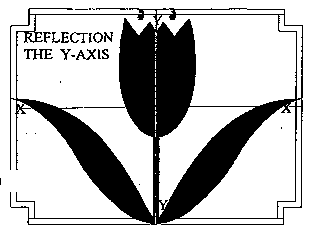
{Figure 1 shows symmetry
with respect to the x-axis while Figure 2 shows symmetry with respect to the
y-axis. This means that the objects look the same on top and bottom, and right,
respectively.}
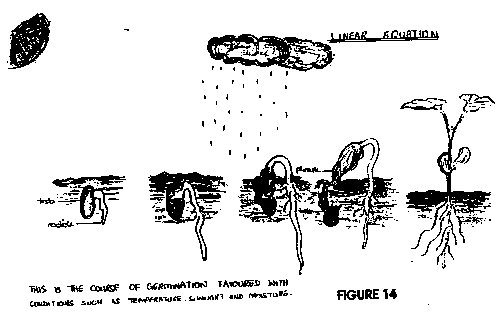
FUNCTIONS

{Figure 3 and figure 4 both
represent functions. This implies that for each input there is a specific
output. Figure 3 compares the human body and a mathematical function while
figure 4 shows a germinating seed receiving various inputs and the output is
its growth.}
INTERSECTION
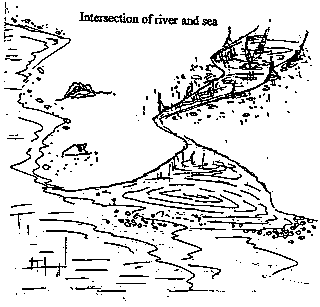
FIGURE 5

{Figure 5 shows the intersection of two bodies of water and the
resulting stream. Figure 6 shows that the natural rise of the wave exhibits the
shape of the square toot function}
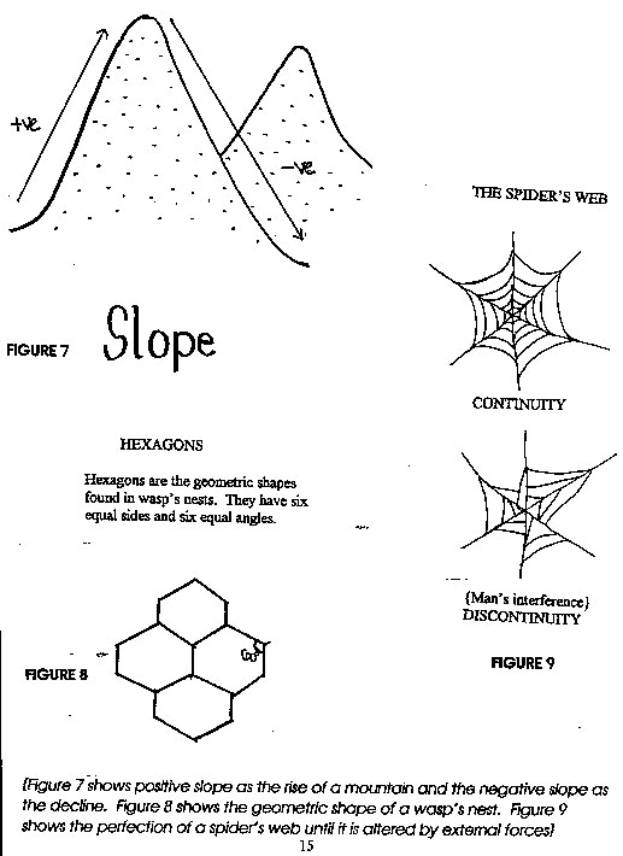

WORKS CITED
Bell, Frederick H. Teaching
and Learning Mathematics (in Secondary Schools). Iowa: W. C. Brown Co.,
1978.
Coffin, Harold G. Creation:
Accident or Design?. Washington,
D.C.: Review and Herald Publishing Association, 1969, p. 41.
Guyer, Michael F. and Lane,
Charles E. Animal Biology. 5th
ed. New York: Harper & Row, Publishers, 1964, p. 74.
Haeussler Jr., Ernest F.,
and Paul, Richard. Introductory Mathematical Analysis (for Business,
Economics and the Life and Social Sciences). 7th ed. New Jersey:
Prentice Hall, 1993, p. 325.
Hill, Barry. Seventh-day
Adventist Secondary Curriculum - Mathematics. 1st ed. November 1990, p. 8, 15-22.
Holy Bible, The (New King
James Version)
Keeton, William T. Biological
Science. 3rd ed. New York: W. W. Norton & Company, 1976, p.
579.
Komiejczuk, Raquel I. And
Brantley, Paul S. "From Creeds to Deeds: Teacher Integration of Faith and
Learning in the Classroom." Journal of Adventist Education.
December 1993/January 1994 Vol 56, No. 2, p. 14 (Previously cited from Frank
Gaebelain (1968) and the South Pacific Division Curriculum Frameworks (1991)
Polya, George. How to Solve It. New Jersey: Princeton
University Press, 1971.
The Seventh-day Adventist
Bible Commentary. Vol 1, Maryland: Review and Herald Publishing Association, p. 217.
Smith, Karl J. The Nature
of Mathematics. 5th ed. California: Brooks/Cole Publishing
Company, 1987, p. 5.
Taylor, John W. "God,
Nature, and Learning: An Integrational Approach." Christ in the
Classroom. Vol. 2., p. 262.
White, Ellen G. Counsels
on Education. Pacific Press Publishing Association, 1968, p. 172.
______________. Counsels
on Health. California: Pacific Press Publishing Association, 1951, p. 19.
______________. Counsels to Parents, Teachers and Students.
Idaho: Pacific Press Publishing Association, 1943, p. 63.
______________. Spiritual Gifts. Vol III - IV.
Washington, D.C.: Review and Herald Publishing Association, 1945, p. 34.
______________. Testimonies for the Church. Vol 3.
California: Pacific Press Publishing Association, 1948, p. 138-9.













