Institute for Christian College Teaching
The Finite, the Infinite, and God
by Wil Clarke
Union College, Lincoln, Nebraska
June 1988
003-88 Institute for Christian Teaching
12501 Old Columbia Pike
Silver Spring MD 20904, USA
The
Finite, The Infinite, and God
In a set theory class in graduate school we
got to discuss Cantor theory. This theory discusses the relative sizes of
different infinities. A nun in the class said to me "God is infinity and
infinity is God". A basic cliché
we all use is that God is infinite. Naturally her statement was an
over-simplification. The comment sparked an interest, however, that has
deepened with time.
Ellen White speaks not only of the infinite value of God, but of sin when she writes: "The infinite value of the sacrifice required for our redemption reveals the fact that sin is a tremendous evil." [16, p 451] Elsewhere she comments that our finite minds cannot hope to comprehend all of the infinity that is God.
The purpose of this paper is to explore a little of what infinity is and how it can influence our understanding of our Creator and our relation to him. Tantalizing pieces can be shared with the students when an appropriate topic arises. Hopefully this will start some of our students thinking.
An incident will indicate
that some have considered this topic of paramount importance. Giordano Bruno,
amongst others, taught that space was infinite. He strongly advocated this
concept in his dialogue of 1584 "On the Infinite Universe and
Worlds." For this he was lured to Venice, captured and turned over to the
inquisition. After 9 years of imprisonment and torture, during which time he
refused to recant, he was burned at the stake. [11, p. 19]
Infinity, as used by Christians, is most often applied as an attribute of God. It is one of those omni - words: omnipotent, omnipresent, and omniscient. It gives visions of eternity, past and present. Always it is the distantly unreachable and mysterious.
Harry Blamires encourages us to explore the unknown.
There is nothing in our experience, however trivial, worldly, or even evil, which cannot be thought about Christianly. To think Christianly is to accept all things with the mind as related, directly or indirectly, to man's eternal destiny as the redeemed and chosen child of God. [3, p. 44, 45].
Almost fifty years ago George McCready Price
urged us to apply modern discoveries to the understanding the character of the
Creator.
All these modern discoveries tend to present the problems of the universe in aspects never dreamed of by the people of the Victorian age. Yet we see little inclination on the part of anyone to make serious use of these new discoveries in trying to understand the character of the Creator, or in attempting to study the ways in which He is conducting His universe. [10, p. 17]
Scripture
A study of the context of for ever, eternal, everlasting, infinity, for evermore, and innumerable, in a concordance of the King James Version of the Bible is essential before we go too deep into the mathematical context of infinity.
In Scripture, these words often have a
relative meaning. By this I mean that there may be expiration. On the other
hand we often take them to mean absolutely what they say. Some examples of
relative use, in a traditional Adventist context are these:
Job is accused of having committed an infinite number of sins [2, Job 22: 5] The armed strength of Ethiopia and Egypt is listed as infinite, and yet they were carried into captivity. [2, Nahum 3:9] There are innumerable beasts, small and great in the sea, and innumerable grains of sand by the seashore. [2, Psalm 104: 25; Hebrews 11: 12].
Jude 7 talks of an eternal fire that consumed Sodom and Gomorrah. Leviticus lists statutes for ever that pertained to the temple ceremonies and passed away with the old dispensation. [see 2, Leviticus 6: 18; 7: 34, 36; 10: 9, 15; etc.]. The Aaronic priesthood, termed an everlasting priesthood in Exodus, is replaced by a more excellent ministry in Hebrews. [2, Exodus 40: 15; Hebrews 8: 6.]
On the other hand these same words are used in a context that we take in an absolute sense. God is an everlasting king. [2, Jeremiah 10: 10]. His understanding is infinite. [2, Psalm 147: 5] And who doubts for a moment that the promise of eternal life in John 3: 16 is not really for ever? If that is not true, then indeed we are of all men most miserable.
From these and other texts it would appear that eternity or infinity is something that lasts a long time or is extremely numerous, and, most importantly, is beyond the power or authority of man to meddle with.
Other Early Views of Infinity
The ancient Greeks used the word apeiron ( apeirwn) for infinity. It appeared to have many negative connotations and none positive. There was no place for the infinite in the world of Plato or Pythagoras. The Pythagoreans believed everything could be described by a finite arrangement of the natural numbers. Aristotle recognized that there were some aspects of the world that might need apeiron. Things such as the flow of time, and the number of points on a line segment might indeed be infinite. He invented the notions of potentially infinite versus actually infinite. Something actually infinite had an air of finality and completeness to it. The set of natural numbers (1, 2, 3...) on the other hand, was only potentially infinite because one never used or needed more than a finite number of them at any one time. Thus he could remain in his own comfortable little finite world without dealing with the unpleasant concept of infinity.
St. Augustine, who adapted Platonic philosophy to Christianity, believed that both God and his thoughts were infinite. This was a bold step beyond believing simply that God was nebulously infinite. Augustine's successors would not go as far as he did. St. Thomas Aquinas gives a circular "proof" that it would be impossible for God to create anything infinite. (A circular proof assumes the result as part of the hypotheses.)
Infinity
George Bernard Shaw once astutely observed that to a bushman who can only count as far as his ten fingers, to him "eleven is an incalculable mystery." [5, p. 42] Of course Shaw was underestimating even the most primitive of the human race. But his point is well taken that infinity is merely something quantitatively beyond our reckoning.
Galileo
Galilei in the early 1600's was the first person to begin to approach infinity
in a modern 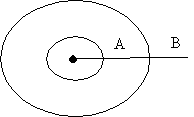 spirit.
He had learned something from Bruno's experience and so was more careful in how
he expressed his scientific sentiments. History documents that he was not
careful enough however.
spirit.
He had learned something from Bruno's experience and so was more careful in how
he expressed his scientific sentiments. History documents that he was not
careful enough however.
Galileo supposed that there were as many points on a 3 inch line as on a 6 inch line. He argued that there were as many points on the circumference of a circle of radious two inches as there were on a circle of radius one inch. To see this, draw the two circles with a common center. Then for every point B on the larger circle there exists a corresponding point A on the smaller circle where the radius from the original point meets the smaller circle. In this fashion every point on the larger circle could be paired with one on the smaller circle. So there must be an equal number of points on each circle, even though the circumference of the larger was twice as long as that of the smaller. This type of reasoning was not fully utilized until Georg Cantor wrote his set theory 250 years later.
Georg Ferdinand Ludwig Philipp Cantor (1845-1918), intrigued by recent non-Euclidean geometry theory, created classical set theory, to put geometry back on track as a respectable branch of mathematics. As part of his set theory he faced the issue of how to count the number of elements in a set. He arrived at the fruitful technique of comparing two sets, element by element. If he ran out of elements in one of the sets first, then that set had fewer elements.
Cantor opened his remarks with the following bold statement:
The fear of infinity is a form of myopia that destroys the possibility of seeing the actual infinite, even though it in its highest form has created and sustains us, and in its secondary transfinite forms occurs all around us and even inhabits our minds. [11, p. 43].
He recognized an absolute infinity. Between this absolute infinity and the finite numbers he created a new class of numbers he called the transfinite numbers.
He denoted the number of integers as w. This is the smallest infinity. Infinite sets have the quality that their elements can be paired with those of proper subsets of themselves. This can, of course, violate our intuition. For example, Galileo used the following pairing to show that there are as many numbers as perfect squares (a proper subset of the set of positive integers):
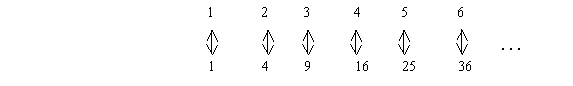
Cantor used the same argument to show that there are no more fractions than natural numbers. However the number of the points on a line segment is greater than w. Thus there are many different infinities each one as much bigger than the previous as w is bigger than any finite number.
David Hilbert used the first letter of the Hebrew alphabet to denote infinity. Thus ÀO (aleph-null) had the same value as Cantor's w. Continuing from there, the set of all subsets of the natural numbers has more elements than the set of natural numbers, so he denoted that infinity as À1. The set consisting of the set of all subsets of the set of all subsets of the natural numbers would be denoted by À2. Furthermore this process can obviously be continued indefinitely.
We can now settle the medieval controversy over how many angels can stand on the head of a pin. If each angel requires but a single point to stand on and there are ÀO angels, the head of the pin could contain all of the angels in the universe. There would still be infinitely more than ÀO points remaining unoccupied!
God is Infinite
This view of an absolute infinity far greater than the ordinary infinities we meet with every day gives us a new and exalted view of what infinity can mean. The eternal life we all look forward to consist of w or ÀO years, but the God with whom we'll spend it represents the only thing we can conceive of as being an absolute infinity.
The famous mathematician and philosopher Bertrand Russell points out that:
the infinity of rationals [w] does not demand, for its definition or use,
any infinite classes or infinite integers. It is not, in actual fact a very
important notion, and we could dispense with it altogether if there were any
object in doing so. The Cantorian [absolute] infinite, on the other hand, is of
greatest and most fundamental importance; the understanding of it opens the way
to whole new realms of mathematics and philosophy. [12, p. 65]
In the context of Cantor's
absolute infinity we quote St. Gregory: "'No matter how far our mind may
have progressed in the contemplation of God, it does not attain to what he is
but to what is beneath him."' [5,
p. 48].
In his worldview James Sire defines a God who is omniscient:
This means that God is
all-knowing. He is the alpha and the omega and knows the beginning from the
end. He is the ultimate source of all
knowledge and all intelligence. He is He Who Knows. The author of Psalm 139 expresses beautifully his
amazement at God's being everywhere, preempting him--knowing him even as he was
being formed in his mother's womb! [13, p. 27].
Sire thus believes that God's knowledge is infinite in at least two dimensions. God knows everything and he knows all time.
In the balance of the paper, I wish to
explore some of the ideas that I have had. Many of these are not original, of
course, but many have occurred to me independently of sources I discovered
later. They should all be read with the following caveat: Our thinking in this
realm is probably as rudimentary as that of the Greek philosophers 2500 years
ago, who believed that all heavenly motion must occur in perfect circles. It
will be very surprising if, in the earth made new, any one or another of these
specific theories described below are found to be true. [Adapted with apologies
to one of this country's greatest astronomers, the late George O. Abell; 1, p. 378]. "Eye hath not seen, nor ear heard neither have entered into
the heart of man, the things which God hath prepared them that love him!"
[2, 1 Corinthians 2:9].
Bounded Infinity
The term-bounded infinity
seems at first sight to be an oxymoron. It refers to the phenomenon mentioned
earlier and stated originally by Galileo that a line segment (which is bounded)
contains many points as any other line segment of any length (bounded or
unbounded). Cantor showed a line segment consists of an uncountably infinite
number of points. Uncountably infinite means a transfinite number greater than
Cantor's w.
Mandelbrot points out that the common land boundary between Spain and Portugal is listed as km versus 1214 km in their respective encyclopedias. [8, p. 33] He attributes this difference to their each using a measuring device with different resolution. In fact the shorter the measuring rod, the longer the boundary. The reason is that the shorter rod will measure more of the irregularities in the boundary. Taken to its logical conclusion, as the length of the measuring rod gets closer and closer to zero, the measured length of the boundary will get larger and larger until it approaches w. Mandelbrot proceeds to define a fractal dimension (or fractional dimension). We will discuss dimension later on.
Nature tends to abound in curves that yield
infinite lengths when measured with infinitesimal measuring rods. Until
recently, mathematics has not concerned itself with irregular curves such as
these. In fact it still does not have a method of modeling such curves. They
are too complicated.
Scientists have defined the chemical
structure of matter in terms of molecules. These in turn are described in terms
of atoms, which were originally considered indivisible. Atoms are now
considered to consist of particles such as protons, electrons, and neutrons.
Recently some of these particles have been subdivided into still smaller
subparticles called quarks. And surely the end is not in sight. Will matter
turn out to be infinitely divisible?
Behind all of this infinite variety in the smallness of nature, we see a Creator. He has a design for nature that goes smaller and deeper than our most sensitive instruments.
Ponder for a moment the mystery of the electron. It's electro-magnetic force is subject to the well known inverse square law. That means that the force quadruples as the distance to the electron is halved. Since the electron is practically dimensionless, an object "touching" the electron would experience an unlimited (infinite) force. Here is an infinite force bound up in an infinitesimal point.
The computer age yields two more examples.
Technology has been squeezing more and more memory into the same physical
dimensions every year. In fact, in recent years, they have doubled the amount
of memory on an integrated circuit every year. Yet computer memory has not
approached that contained within the human mind in either capacity or ease of
accessibility. God has enabled our brains to remember an apparently unlimited amount
of knowledge. Although the human body
and mind have degenerated considerably since the perfection of creation, we are
still blessed with far more memory capacity than we ever use.
But God knows the name of every star [2, Psalm 147: 4; Isaiah 40:26]. Scientists
tell us that are probably at least 300 billion stars in our galaxy alone. [14, p.422] To get a slight feeling how big that number is, suppose we gave
each star a word out of the Oxford English Dictionary for a name. We would run
out of names at about 500 thousand stars. How many of us know even 20% of that
number of English words? The United Nations estimates that there are about 2000
different languages in the world. If every language had as rich a vocabulary as
English (and most don't) and we used dictionaries of each of these languages to
names the stars in our Milky Way galaxy we could name about 1 billion stars.
That is less than one per cent of the stars galaxy alone. Furthermore there are
over 200 billion known galaxies of stars. Now marvel at the memory that knows
all of that and at the same time knows exactly how many hairs you have on your
head! Are we viewing a memory that just
might be infinite? I believe we are.
When people think of computers, they normally think of speed. Today we measure the speed of computers in MIPS (millions of instructions per second). For example the Macintosh computer I am typing this paper on is rated at about 8 MIPS. My old Apple II+ was rated at about 1 MIPS. Newer and faster computers run at much higher MIPS rates. What we are doing is squeezing more and more processing into each second. I believe that God must have the ability to do an infinite amount of processing in any given time period. The amount of data handled needs to be measured in the realm of ÀO at least and maybe some higher Àn is required. Like some of the new modern computers and like the human brain, God's mind must be able to process many things in parallel (simultaneously). Again I believe that he must be able to handle at least ÀO unrelated thoughts simultaneously.
Unbounded Infinity of Time
As
the doctrine of the eternal existence of God began to dawn on my childhood mind
I was utterly intrigued. Everything in our experience has a beginning. And so
my question was "What happened before that?" People suggested I think
about a ring, because it has long been a symbol of infinity, having neither
beginning nor end. But, that didn't help a bit.
St. Augustine asked himself what God was doing before he made heaven and earth, to which he replied "He was creating hell for people who ask questions like that!" [7, p.112].
Looking out at the nighttime heavens we see objects that are thousands of light years distant. This implies that these objects existed long before the 6,000-year-old beginning of the heavens and earth. A simple minded explanation is that when God made the stars he made them with apparent age, that means that he made their light beams throughout the universe at the same time he made them. After all, didn't he make Adam and Eve and their garden home fully mature, with every evidence of age?
Even our simple minded answer, however, leaves us with St. Augustine's nagging question, what was God doing before then? In God and the Astronomers Robert Jastrow traces the tortuous trail of modem cosmology. He shows how the galactic red shift forced Astronomers to draw an obvious conclusion. The apparent interpretation of the red shift is that the universe is expanding. Now simply trace this expansion backwards to the time when all these lines of expansion converge and you come up with a date. This date, 10 to 20 billion years ago, would seem an obvious choice for the beginning of time in our universe. The event is referred to as the Big Bang. There are two straightforward methods of arriving at this date. One points to about 20 billion years ago, the other to about 10. But the allowance for error in each approximation overlaps the other, so no one is worried about the discrepancies, yet. This forced scientists to accept that the universe did have a beginning; it has not always been here. Jastrow states, albeit reluctantly, that the modem scientist has scaled the mountains of ignorance; he is about to conquer the highest peak-, as he pulls himself over the final rock, he is greeted by a band of theologians who have been sitting there for centuries! [7, p. 116]
Naturally he places the
creation of the universe at the time of the Big Bang. Of course neither
creationists nor evolutionists believe the earth was created at that time.