MATHEMATICS
A Curriculum Framework for
Seventh-day Adventist Secondary Schools
Mathematics
Curriculum Framework
Third Edition June 2000
ACKNOWLEDGEMENTS
The
South Pacific Division Curriculum Unit has enlisted the help of a number of
teachers in preparing this document. We
would like to thank all who have contributed time, ideas, materials and support
in many tangible and intangible ways.
In particular, the following people have helped most directly in the writing
and editing of this document:
First
Edition 1990
Lyn
Ashby Doonside
Adventist High School
Mike
Bartlett Carmel Adventist
College
Chris
Cowled Oakleigh Adventist
School
Rae
Doak Sydney Adventist
High School
Allan
Dalton Lilydale Adventist
Academy
Gordon
Howard Avondale
Adventist High School
Karen
Hughes Auckland Adventist
High School
John
Oxley Brisbane
Adventist High School
Graeme
Plane Murwillumbah Adventist
High School
Alastair
Stuart Longburn Adventist
College
Steve
Walker Carmel Adventist
College
Stan
Walshe Longburn Adventist
College
Robert
Wareham Nunawading Adventist
High School
Roddy
Wong Sydney Adventist High
School
Second
Edition 1999
Lyndon
Chester Tweed Valley Adventist
College
Malcolm
Coulson North NSW Conference
Education Director
Stephen
Littlewood Border Christian College
Ralph
Luchow Tweed Valley
Adventist College
Craig
Mattner Carmel Adventist
College
Ray
Minns Northpine
Christian College
Wilfred
Pinchin Avondale College
Robert
Wareham Nunawading Adventist
College
Third
Edition 2000
Ray
Minns Northpine
Christian College
It
is our wish that teachers will use this document to improve their teaching and
so better attain the key objectives of Seventh-day Adventist education.
Sincerely
Barry
Hill
Director,
Secondary Curriculum Unit
South
Pacific Division, Seventh-day Adventist Church
Department
of Education
148
Fox Valley Road June
2000
WAHROONGA
NSW 2076 Third
Edition
Table of Contents
table of
Contents . .. .. . . . . 4
section 1 introduction. . . .. . . . . 5
section 2
philosophy . . . . . .. 8
3.1 Steps in Planning Units and Lessons . . . . . 13
3.2 Sample Units of Work -
Probability . . . . . 15
- Statistics . . . . . . . 16
section 4
planning elements . ... . . . 17
4.1 Ideas for Teaching Mathematics in a Christian Context . . . 18
4.2 List of Mathematical Processes and Skills . .. . . 27
4.3 Detailed Objectives of Mathematics . . . . . 28
4.4 Values and Concepts in Mathematics Topics . . . . 30
4.5 Attitudes to Classwork . . . . . . . 37
4.6 Assessment . . . . . . . . 39
section 5
appendices . . . .. . . . 41
5.1 What are Values? . . . . . . . 42
5.2 A Christian Approach to Values . . . . . . 42
5.3 A Christian Approach to Teaching Mathematics .. . . . 43
SECTION 1
Introduction
INDEX
1.1 What is a Framework? . . . . . 6
1.2 Using the Framework . . . . . .7
1.1 what is a Framework?
In the Adventist secondary school context, a
“framework” is a statement of values and principles that guide curriculum
development. These principles are derived from Adventist educational philosophy
which states important ideas about what Seventh-day Adventists consider to be
real, true and good.
A framework is also a practical document intended to
help teachers sequence and integrate the various elements of the planning
process as they create a summary of a unit or topic.
The framework is not a syllabus.
The framework is not designed to do the job of a
textbook. Although it contains lists of
outcomes, values, and teaching ideas, the main emphasis is on relating values
and faith to teaching topics and units.
One objective of the framework is to show how
valuing, thinking and other learning skills can be taught from a Christian
viewpoint. The Adventist philosophy of Mathematics influences this process.
A second objective is to provide some examples of
how this can be done. The framework is
therefore organised as a resource bank of ideas for subject planning. It provides ideas, issues, values and
activities to teach these.
The framework has three target audiences:
1.
All
Mathematics teachers in Adventist secondary schools.
2.
Principals
and administrators in the Adventist educational system.
3.
Government
authorities who want to see that there is a distinctive Adventist curriculum
emphasis.
1.2
Using the Framework
Before attempting to use this document for the first
time, it is suggested that you read through this whole framework.
Notice that the framework is comprised of the
following:- explanation of a framework and its use, philosophy and objectives,
suggestions on how to plan units of work, key planning elements, examples of
topic plans, lists of important ideas, values, issues, teaching strategies, and
other elements which are useful in building a planning summary.
These components are grouped into five
sections. The nature and purpose of
each section are set out below.
Section 1 – introduction
Section one sets out the purpose of having a
framework. It explains what a framework
is and shows how to use it in a teacher’s program and on a regular basis to
enhance one’s teaching and make it more Christian oriented.
Section 2 – philosophy
This is the philosophical section. It contains a philosophy statement, a
rationale ( a statement of the value base for teaching mathematics), and a set
of objectives which have a Christian bias.
This section is meant to help teachers refresh their
memories of the Christian perspective they should teach from. They may consult this section when looking
at longer-term curriculum planning, and when thinking about unit
objectives. They may also consider the
adapting it or using it to form part of their program of work.
Section 3 – planning a unit of work
Section three is of the “how-to” section of the
framework. It explains procedures
teachers can follow when planning an overall course, topic, or unit of work
while thinking from a Christian perspective.
It ends with sample units of work compiled after working through the
steps. Because it suggests ideas for integrating knowledge, values and learning
processes in teaching, this section is the heart of the document.
Section 4 – planning elements
This section contains the various lists of ideas, values and teaching
strategies that teachers may consult when working their way through Section
three of the framework. It is a kind of
mini dictionary of ideas to resource that steps followed in Section three.
Section
5 – appendices
Section five
contains ideas for teaching that may lie outside the immediate context of the
classroom. It assists teachers in
explaining in more detail some of the more specific ideas and approaches
presented in this framework. It
examines the meaning of values and how a Christian should approach values in
mathematics, both of which are useful as reminders of good teaching and
learning practice.
SECTION 2
Philosophy
INDEX
2.1 A Philosophy of Mathematics . . . . 9
2.2 Rationale . . . . . . . . 10
2.3 Mathematics Objectives . . . . . 11
2.1 a philosophy of mathematics
Everywhere in nature there are evidences of mathematical
relationships. These are shown in ideas
of number, form, design and symmetry, and in the constant laws governing the
existence and harmonious working of all things. Through its study of these laws, ideas and processes, mathematics
can reveal some of God's creative attributes, particularly His constancy.
Whereas the student cannot comprehend the absolute
unchangeable nature of God, mathematical dependability demonstrates clearly the
consistency of God and His perfect creation.
This is a demonstration of total dependability.
Mathematics may also develop students' capacity to
use appropriate thought processes to more clearly identify aspects of truth
which relate to natural laws and design.
Such truth is predictable, in that given a set of axioms and the
appropriate mathematical processes, the result is always as expected. Therefore when students learn mathematical
processes, axioms and laws, they may be further enabled to more clearly
identify God's design and handiwork in nature.
While mathematics is a pure science, allowing many hypotheses and
conjectures to be conclusively demonstrated as being either correct or
incorrect, it also opens possibilities of knowledge that defies either proof or
disproof. Examples are infinite
smallness and infinite greatness. This
unusual balance between the unexplained and the clearly evident provides the
student with an accurate picture of an infinite and eternal God, whom we can
neither prove nor disprove, yet in whom we believe. However, God has created rules and functions that can be
demonstrated as an evidence of His presence.
As the language of the universe, mathematics helps
show us how God is made manifest there.
It expresses this part of God’s quality in its patterns of space and
number that are partly aesthetic and spiritual. The spiritual dimension of mathematics transcends logic and
reason. It asks ultimate questions,
reveals the marvels of human imagination, presents amazing ideas, and changes the
way we think about the world.
2.2 rationale
There are many reasons why students should learn
mathematics.
Firstly, they need to master basic mathematical
skills in order to cope with the demands of life. Such demands include being numerically literate, gaining the
tools for future employment, developing the prerequisites for further
education, and appreciating the relationship between mathematics and
technology.
Secondly, mathematics is the language of the
sciences, and many disciplines depend on this subject as a symbolic means of
communication.
Thirdly,
a particularly important life skill is decision-making. Mathematics education can play an important
part in developing students' general decision-making and problem solving
skills.
A fourth justification for learning mathematics is the need for students
to use the subject as an important means of discovering truth. The discipline clearly and precisely
presents aspects of knowledge which are helpful in finding out truth about the
structure and patterns of the environment, and of some of the ways in which God
has communicated with man.
The fifth reason for studying mathematics is closely
associated with the quest for truth. It
is that mathematics assists our search for beauty. Students develop their aesthetic aptitudes by looking at patterns
in nature and by appreciating the precision and symmetrical beauty in God's
creation.
The
sixth justification for mathematics is that it is an important aid in
developing the creativity of the individual.
Here the student has limitless opportunity to test his skills against
the immutability of God's law. In a
very real sense the student will develop confidence as he or she examines the
consistency of law.
2.3 mathematics objectives
The study of mathematics aims to enable students to:
1.
Develop
willingness to perceive the spiritual dimension in mathematics.
2.
Develop
an awareness that mathematical order and precision are characteristic of God
the Creator.
3.
Develop
a growing knowledge of God's faithfulness and dependability through studying
mathematics as a language of the universe.
4.
Develop
the ability to make links between mathematical concepts and other aspects of
experience, whether these aspects are largely intellectual, practical or
spiritual.
5.
Develop
the ability to identify values and make value judgments about mathematical
ideas and quality.
Attitude
to Mathematics
1.
Perceive
mathematics as a living art, one which is intellectually exciting,
aesthetically satisfying, and relevant to applications which help meet life
needs.
2.
Develop
a positive, adventurous attitude to learning mathematics, which includes
enjoyment of learning.
3.
Appreciate
the value of calculating devices in mathematics.
4.
Develop
a positive set of emotional competencies through learning mathematics. Examples
are self-discipline, self-confidence, patience, and courage.
Learning
of Mathematics
1.
Use
mathematics in coping with, controlling and determining factors which will
influence their present and future environments.
2.
maintain and increase their range of basic mathematical skills.
3.
develop the ability to communicate using the symbolism and procedures of
mathematics.
4.
Develop
competence in applying mathematics in a wide variety of life situations.
5.
Develop
the skills of logical thinking and presentation.
6.
develop the synthesis skills of using techniques from different areas of
mathematics to solve a problem.
7.
develop skills in talking, listening, reading and writing about
mathematics.
8.
support other fields of study which make use of mathematical techniques.
SECTION 3
Planning a unit
of work
3.1 Steps in Planning Units and Lessons . . . 13
3.2 Sample Units of Work - Probability . . . 15
- Statistics . . . 16
3.1 steps IN PLANNING units AND LESSONS
When planning courses, units and lessons, there are
some essential planning elements to keep in mind. Suggestions for going about the planning process are set out
below.
On the following pages there are examples of how
unit plans may appear in work programs.
A Overview
1.
Read
government requirements to find the syllabus requirements, content to cover,
objectives, scope and sequence. These
will be unique to each state, although there will be some degree of similarity
in junior school with the recent moves towards a national core outcomes-based
curriculum.
2.
Fit
the topics to the school calendar and weekly timetable to create units of
work. Take into account public
holidays, exam blocks, revision time for tests/exams, school camps, sporting
days, school photos, competitions, known excursions, and any other form of
known interruption. It is always best
to gain the yearly picture to determine what can and cannot be covered for the
teacher’s as well as the student’s sanity.
Ensure topics are not rushed by allowing some extra time every so
often. By doing this, unexpected events
such as excursions can be compensated for and one’s anxiety will be reduced.
B Composing a Topic
1.
Gather
information on the topic, including possible texts and resources. Contact your local Education Department,
especially the subject Curriculum Development Officer. Ring other schools in your district and talk
to teachers in your subject area. Most
teachers are more than willing to help.
2.
Refer
to Section 4 for outcomes in each of the four areas of knowledge, skills,
higher processes, and values that you could incorporate into your unit of
work. Section 3.2 has sample units of
work. Try to compose your unit of work
from a Christian framework.
3.
Start
to think about the main assessment tasks of the unit. Think beyond the standard test.
Try to cater for individual differences in assignment. In Section 4.5 you will find a range of
ideas.
4.
Break
the information into lessons with appropriate time for the elements to be
covered each lesson. Allow time for
activities (in or out of the classroom), for possible research or computer
time, and for revision.
5.
Sequence
the lessons with appropriate links between them.
C
Individual Lessons
1.
List
the most important outcomes. Knowledge
outcomes include content, and the concepts and worldview of mathematics. Skills outcomes describe abilities that
follow knowledge and practice. Higher
Processes include elements of processes such as inquiry, problem solving and
data processing. Values are of many
kinds. See .those in Section 4.1. Some
are teachable more directly and others are taught less directly by exposure and
experience. Some are assessable, and
some are not.
2. Determine how
these outcomes (knowledge, skills, higher processes, values) will be achieved.
3.
Devise
interesting teaching strategies and look for supporting resources.
4.
Create
and refine teaching notes.
D Post
Lesson Planning
1.
Evaluate
during and after teaching. Make notes
where you can improve for next time.
2.
Modify
future teaching.
SECTION 4
Planning elements
4.1 Ideas for Teaching Mathematics in a
Christian Context . . . . . . . 18
A Teach
the Idea of Quality . .. . . 18
B Teach
Values – types, tactics . . . . 18
C Teach
About Wonder and Spirit . . . 20
D Make
Links Between Math’s Concepts,
Experience and the Christian
Worldview . 20
E Use
Biographies to Teach Values, Concepts
And Wonder . . . . .. . 21
4.2 Lists of Mathematical Processes and Skills . . 27
4.3 Detailed Objectives of Mathematics . . . 28
4.4 Values and Concepts in Mathematics Topics . 30
4.5 Attitudes to Classwork . . . . . . 37
4.6 Assessment . . . . . . .. . 39
A Teach the Idea of Quality
Remembering that God’s quality is the foundation of
Christian reality, teachers can cmphasise the idea that mathematics teaches
particular aspects of this quality.
This helps bring together the Christian and mathematical worldviews.
Consider the following ideas about how mathematics
expresses the quality inherent in the space and numbers of the universe.
3.
Mathematics
is the science of space and number. Space and number have important value in
themselves, and help create the quality of our life.
4.
Mathematics
is a language that describes the properties of the universe. Through it we
better understand the quality and reality of the created universe.
5.
Mathematics
is a numerical pattern of values.
6.
Mathematics
requires rigorous thinking about number, axioms, laws etc. This is a kind of
intellectual quality.
7.
Mathematics
helps us understand and use science and technology. These in turn add quality to daily life.
8.
Aesthetic
quality is shown in number patterns.
5.
Mathematics
gives us quality of understanding about the world — a clearer world view
B Teach Values
1. Types
of Values
Types
of values that are derived from the reality of Mathematics are listed
below. Although the values are
categorised in a particular group, many could be placed in several categories.
Aesthetic
Values
6.
Appreciation
of a Designer
7.
Awe
of the imagination beauty and power of mathematics
8.
Balance
in mathematical properties and design
9.
Economy
of design in nature
10.
Elegance
of a solution
11.
Harmony
in design and beauty
12.
Mathematical
harmony in music
13.
Order
of numerical patterns and working
14.
Sense
of beauty
Application to
Life Values
1.
Ability
to apply mathematics - in managing money, going shopping, calculating
dimensions of things etc
2.
Appreciation
of the practicality of mathematics
Creativity
Values
1.
Ability
to design
2.
Ability
to see and create problems
3.
Flexibility
4.
Originality
in solving problems
Emotional Values
1.
Desire
to develop one’s ability
2.
Perseverance
3.
Positive
attitude to mathematics
4.
Positive
sense of self-worth
5.
Positive
use of difficulty and failure
Intellectual
Values
·
Ability to
arrange priorities
·
Ability to
make good choices and decisions
·
Acceptance
of paradox
·
Accuracy
·
Application
ability
·
Appreciation
of inquiry in learning
·
Awareness
of choices and their consequences
·
Awareness
of the potential of mathematics
·
Care in
work
·
Caution in
interpretation of data
·
Clarity of
reasoning process
·
Disciplined
memory
·
Disposition
to learn from mistakes
·
Disposition
to search
·
Economy of
working method
·
Economy in
use of resources
·
Logic
·
Open
mindedness
·
Perspective
of the certainty of mathematical ideas and laws
·
Predictability
of mathematical laws
·
Progressiveness
·
Responsibility
for quality
·
Stewardship
of resources, time and effort
·
Verification
of procedures and results
Social Values
5.
Appreciation
of human mind and imagination
6.
Appreciation
of the inner logic of mathematics
7.
Awe
of the power and beauty of mathematics
8.
Disposition
to find evidences for God
9.
Interest
in asking ultimate questions such as “what is finite and infinite?”
10.
Reference
to ethical principles
11.
Wonder
about properties of space and number
Section 4.3 lists many mathematical topics and
identifies values that could be communicated in those topics.
2. Tactics for Teaching Values
·
Identify
values involved in problems and examples.
An example is the value of stewardship which is careful budgeting, and
the responsible use of funds through credit cards etc. When we are teaching aspects of how
mathematics affects consumers, we may emphasise the importance of stewardship.
·
The making
of choices and decisions is an important part of valuing. We can emphasise the idea that mathematics
involves many decision-making situations.
For example students make choices about the best procedures to solve
problems. We may refer to the
consequences of making such decisions, and ways of verifying that these
consequences will occur.
·
An
extension of Point 2 is to teach the idea that in mathematics we make value
judgements about the worth of problem solutions or procedures we use. In this kind of situation we are focusing on
quality in our working procedures. This
kind of quality is also linked to intellectual values such as accuracy and
clear logic
·
Look for
opportunities to teach values in appropriate topics. An example of a values-oriented topic is how mathematics
influences beauty and design in nature.
·
Consciously
model what it is to be a mathematician of quality. Such modeling includes personal ethics, the approach to doing
mathematics, and social interaction.
·
Teach
attitudes to being a good scholar in classroom procedures and interaction.
C Teach About Wonder and Spirit
Mathematics is more than reason. Like many other forms of knowledge, it has a
spiritual dimension. Teachers can start
to point students to this dimension by using opportunities to mention aspects
of mathematics that are potentially spiritual in nature. Examples:
·
Mathematics
reveals remarkable feats of human imagination that go beyond common sense and
immediate reality. This means they can “transcend” in one kind of spiritual
sense.
·
Mathematics
is deeply human because it shows the marvels of the human mind in operation.
Our humanity is itself a thing of awe.
·
Mathematics
is spiritual because it asks ultimate questions such as “what is finite and
infinite?”
·
Mathematics
is a thing of wonder because it is essentially the language of the universe.
·
Mathematics
is astonishing because it presents amazing ideas such as negative numbers.
·
Mathematics
is majestic and powerful because it has an inner logic that looks as if a
single intellect is in operation when developing mathematics, when in fact
there are many.
·
There is
spiritual quality in human awe and wonder about properties of space and number.
D Make Links Between Math’s Concepts, Experience and the
Christian Worldview
Teachers can make links between the concepts of
mathematics and aspects of experience. Major mathematical concepts include
infinity, equality, and uncertainty.
Linkages can be made by using analogies, parallels,
comparisons and object lessons. The following examples illustrates this
strategy.
One concept is infinity. The idea of infinity is a
concept, not a number. It is something that has no limits, and which is
unbounded or unreachable. The unknown infinite “nothings” of mathematics are
turned into something through calculus. One example from the natural world is
the idea of “cosmos.”
Another concept is balance. Solving equations always
requires them to be balanced. An unbalanced or messy sequence ends in the wrong
answer. In reference to life, imbalance can result in an unhealthy lifestyle.
Also, a satisfying Christian life always requires a balance.
A question format can help this linkage process. An
example of using a question is:
·
Is infinity
a concept or a number?
·
In what
ways is infinity a metaphor for your concept of God?
It is important to recognise that some links in this
process are inherent and others analog. To illustrate, the concept of
“logarithms” models the way we respond to the intensity of sounds. This is an
inherent link between mathematics and experience.
By contrast there is an issue of “Christmas” being
abbreviated as “Xmas.” We may think about the idea that the “X” in “Xmas” can
be seen as an unknown like an “x” in an equation. To use an indirect analog
link, we could say that Christmas has changed its focus, no longer with the
focus being on “Christ”, so that it has also become an unknown.
The aim in this kind of process in this framework is to provide teachers
with ideas, yet at the same time to avoid derision for being simplistic or too
ambitious. It is important not to claim too much when making links between the
mathematical worldview and the Christian worldview.
The next six pages give more inherent and indirect
links between ideas and values of mathematics, and the Christian worldview.
E Make Links Between
Values and Christian Worldview
This section of the framework attempts to show how teachers can make
links between mathematical concepts and values and ideas that are found in
life’s experience, and that are often outside mathematical study. Some of the key concepts of mathematics are
set out below in table form to align each concept with its possible applications.
|
Concepts
|
Applications
|
|
Absolute Value
|
|
|
Absolute
Value
|
Inherent Link
Indirect Links
God
is absolute
God
turns negatives into positives
Quadratics
– frowns can be turned into smiles
|
|
Comparisons
|
|
|
Equations
and inequations
Balance
Opposites
Greater
than and less than
Inverses
Real
and unreal
Terminating
and non-terminating decimals
Digital
and analog
|
Inherent Links
Discrimination
involves comparison
Conservation
laws and their limits (mass/energy) show boundaries between variables and
invite comparison
Value
equivalence rather than
“appearance” may better express identical properties
Indirect Links
Good
and evil can compare with infinite and finite
Real
and unreal can compare with love and hate
Truth
and error are opposites
Conditional
equality can depend on circumstances
Value
– God’s idea of value is different from ours
Comparison
between the transition from OT and NT and progress in personal development
|
|
Concepts
|
Applications
|
|
Data
|
|
|
Qualitative and quantitative
Statistical procedures
Sampling
Graphs
Numbers
Organisation
Estimation
Simulation
Statistical measures
Normal curve
|
Inherent Links
Each
piece of information has equal significance
Honesty
in representation of data is important
Indirect Links
One
person as a single entity can make a difference
Life
on this earth is only a sample of the real Christian life still to come
|
|
Infinity
|
|
|
Has
no limits, unbounded, unreachable
A
concept, not a number
Can
refer to number lines (big, or small)
The
unknown
Related
concepts – fractions, decimals, asymptotes
|
Inherent Links
Infinite
“nothings” are turned into something from calculus
One
example from the natural world is the idea of “cosmos”
Indirect Links
Infinite can
be “inside” finite. An example is
incarnation (a finite God in a finite body)
It
is one of the different metaphors for God
It
can relate to God’s beginning or end
It
does not reduce God but increases understanding of him
It
can express time and the relationship to God
|
Concepts
|
Applications
|
|
Logic
|
|
|
Way
of thinking and doing
Order
of operations
Provides
linkage between ideas (eg reasoning/setting out)
Undergirds
laws of Mathematics
Depends
on suppositions and assumptions
Includes
proofs and induction
Has
conventions
Grouping
of lie terms
|
Inherent Links
Logic
shows the juxtaposition of design and chance
Logic
expresses conventions versus absolutes
Fairness
relates to logic
Indirect Links
There
is choice in logic as in salvation
There are
arbitrary human limits to logical limits
The
brain has a self-organising function relating to logic
The
brain has a self-organising function relating to logic
There
is logic in consequences for choices
The
conditionally for salvation is not logical
|
|
Measurement
|
|
|
Time
Space
– length / area / volume
Mass
and weight
Pi
Angles
Trigonometry
Speed/acceleration
Estimation
Measurement
systems
Reference
points
Logarithms
Use
of aids like calculators and rulers and instruments
Limits
of accuracy
|
Inherent Links
Relativity
is a kind of measurement perspective
There
is relationship between linear time and space
Judging
involves measuring things like scales and reference points
Indirect Links
Short
time gaps such as in God’s travelling (eg Gabriel and Daniel) are amazing
Concept
of spiritual warfare has certain kinds of dimensions
Time
is ever new, involving decisions and ramifications
Omnipresence
cannot be measured
God
not limited by time and space
Prayer
– how does God cope with the immeasurable?
Limited
or choice? Destiny – predetermined, measured, God measures Christ rather
than us
Prophecy
and time are related measures
Perfection
seems immeasurable
The
relation between design skill and extent of experience is measurable
Age
of the earth is hard to measure
Bible
study is an aid to measurement
|
|
Concepts
|
Applications
|
|
Number Systems
|
|
|
Natural
Rational
Irrational
Real
Imaginary
and complex numbers
Number
bases
Images
Zero
Binary
Decimals
and place value
Fractions
Sets
and subsets
|
Inherent Links
Going
through operations without understanding does not use the potential of number
systems
Every
set is a subset of something bigger
Imaginary
numbers have a physical reality
Indirect Links
Small
discoveries such as number have made large differences in our lives
No
persons should feel insignificant because small things like numbers are not
God
is the universal set
Time-based
cycles of day, year, month are defined in nature, but where did the week come
from?
Once
a person accepts Christ, experiences become real (like or unlike a number
system?)
|
|
Patterns
|
|
|
Sequences
– Fibbonacci; GPs and Aps
Fractals
Tessellation’s
Aesthetics
Design
and design process
Spirals
Repetitions
Modeling
Symmetry
|
Inherent Links
Examples
of patterns: exponential growth and decay; normal distribution; patterns in
mathematical functions and their graphs
Harmony,
beauty, symmetry and patterns abound
Patterns
of mathematics are numerical value patterns
Indirect Links
The
intrinsic value of mathematics is shown by its practical value to people
Design
implies a designer
|
|
Concepts
|
Applications
|
|
Proofs
|
|
|
Different
types of proofs – contradiction; induction; direct
Evidence
and example
Axioms
and theorems
|
Inherent Links
Evidence
can be internal, not necessarily external
The
lack of a proof does not mean that something does not exist
Indirect Links
Contrast
of evidence and proof is required to allow room for faith
God
chose to work with evidence, not proof
Proof
by Mattner re conversation with God – still have to accept him at his word
|
|
Proportions
|
|
|
Ratios
Aesthetics
Design
Dimensions
Direct/indirect
variation
Inverse
variation
Fractions
and percentages
|
Inherent Links
Aesthetics,
the sense of the beautiful contains proportions
Present
in design in nature such as in the Fibbonacci series
Inverse
square laws show proportion
Indirect Links
Creativity
depends on design and variation
Human
perception is not necessarily accurate
|
|
Similarity/Congruence
|
|
|
Similarity
Equivalence
Reasons
for congruence
Grouping
of like objects
|
Inherent Links
Indirect Links
Man’s
likeness to God
Race,
language, and philosophy have congruence
There
is congruence between mathematics and world view
|
|
Concepts
|
Applications
|
|
Transformations
|
|
|
Translation
Rotation
Reflection
Symmetry
Enlargement
Shear
Matrices
and vectors
Objects
and images
|
Inherent Links
Indirect Links
Transformation
of a life parallels mathematical transformations
Reflection
of Christ a transformation
Incarnation
is a transformation
Perception
can involve transformation
Turning
a life around – conversion is transformation
God
is required for direction, enlargement, translation in life
|
|
Uncertainty and probability
|
|
|
Chaos
Chance
Sequences
Complement
Confidence
intervals
Predictability
Margins
of errors
Odds
Binomial
Theorem
Probabilities
of zero and one
Dependent
and independent events
Qualitative
and quantitative
|
Inherent Links
Decision-making
draws on probability
Indirect Links
Beliefs
about life views involve probability
Certainty
of beliefs such as about religious salvation relate to probability
Creation
and evolution debate the probability of one kind of beginning over another
Gambling
with probability involves stewardship
God’s
existence has probability
God’s
involvement in things that seem to have no rhyme or reasons expresses
uncertainty or probability
Parable
of the sheep and the goats expresses probability
Pascal’s
Theorem weighs up the probability of God
Success
or failure are the only two probability options in some aspects of life
|
|
Concepts
|
Applications
|
|
Variables
|
|
|
Express
abstract quantity
Representations
of something else
Provide
the ability to generalise
Subject
to laws and boundaries
|
Inherent Links
Variables
express an unknown quality
Variables
help us derive an understanding or appreciation for something initially not
known
Indirect Links
The
abbreviation Xmas rather than Christmas
shows representation of the spiritual unknown in the actual event
Christ’s
representatives on earth are variables
We
are subject to natural laws like variables are
|
F Use Biographies to
Teach Values, Concepts and Wonder
The lives of mathematicians provide opportunities to
teach values. Consider the following example of how biography can be used to
introduce values and worldview ideas.
The issue of how we gain certainty about what is
real raises the question of what really lies at the heart of maths. For example
Robert Pirsig has explained how the Frenchman Poincare changed his ideas about
the nature of maths. He was puzzled by Euclid’s fifth postulate that said that
through a given point there’s not more than one parallel line to a given
straight line. He saw that Lobachevski had refuted this postulate as impossible
and set up his own geometry which was as good as Euclid’s. Then he noted that
Riemann appeared with another unshakable system which differed from both Euclid
and Lobachevski. An “aha” experience happened when contrary to his previous
thinking he realised that his system of mathematical functions called the
“Theta-Fuchsion Series” was identical with non-Euclidian geometry.
Poincare concluded that the axioms of geometry are
simply conventions and not proven facts. We choose among them to obtain what
suits us if it is advantageous to us. Even concepts such as space and time are
only changeable definitions chosen on the basis of their convenience.
He then struggled with questions like “what are the
most important facts?” and “how de we choose the best facts?” In the end he
decided that mathematical solutions are selected by the subliminal self on the
basis of “mathematical beauty” of the numbers and forms, of geometric elegance.
He said “this is a true aesthetic feeling which all mathematicians know… but it
is this harmony, this beauty that is at the centre of it all” (Pirsig 1974,
270).
Bibliography. Pirsig, Robert. 1974. Zen and the Art of
Motorcycle Maintenance. Viking.
Set out below are a number of processes and skills that could be taught
in secondary mathematics courses. The
list is not exhaustive, and is meant to help teachers see at a glance a profile
of skills that a student would try to develop over time.
|
Processes
|
General
|
|
Approximation
|
Application
|
|
Calculation
|
Constructing
|
|
Communication
|
Drawing
|
|
Data processing
|
Graphing
|
|
Decision-making
|
Manipulating
|
|
Estimation
|
Measuring
|
|
Exploration
|
Risk taking
|
|
Inquiry
|
Using computers
|
|
Problem solving
|
|
|
Thinking
|
Inquiry
|
|
|
Investigating
|
|
Skills
|
Listing
|
|
|
Multiple references
|
|
Calculation
|
Seeking patterns
|
|
Performing calculations
|
|
|
Substituting
|
Problem
Solving
|
|
Using a calculator
|
Analyzing information
|
|
Verifying results
|
Looking ahead
|
|
|
Looking back
|
|
Communication
|
Problem discovery
|
|
Comparing
|
Seeking information
|
|
Comprehending
|
Synthesizing
|
|
Describing
|
|
|
Explaining
|
Social
|
|
Following instructions
|
Accepting responsibility
|
|
Neatness
|
Contributing
|
|
Representing
|
Following directions
|
|
Setting out
|
Initiative
|
|
Sketching
|
Listening
|
|
Terminology
|
Persevering
|
|
Writing skills
|
Tolerance
|
|
|
|
|
Data Processing
|
Thinking
|
|
Classifying
|
Abstracting
|
|
Collating
|
Analysing
|
|
Collecting data
|
Classifying
|
|
Organizing information
|
Comparing
|
|
Presenting
|
Deducing
|
|
Recording
|
Generalizing
|
|
Summarizing
|
Inferring
|
|
|
Synthesizing
|
|
|
Validating
|
|
|
Mental arithmetic
|
|
|
Patterning
|
|
|
Plotting
|
4.3 OUTCOMES
OF MATHEMATICS
KNOWLEDGE
Students should be
able to:
1. Recall mathematical facts;
2. Understand and use mathematical
terminology;
3. Understand mathematical concepts and
relationships;
4. Understand the historical contribution of
mathematics to society;
5. Know relevant formulae, equations, rules
and theorems and their proofs when appropriate;
6. Know relevant procedures and techniques
such as the method of proof by induction;
7. Recall
basic shapes of the graphs of the functions and relations used;
8. Understand where mathematics is used in
real life.
LARGER
PROCESSES
Students
should be able to:
1. Access the appropriateness of a particular
strategy in solving a problem;
2. Identify and execute the discrete steps
necessary to solve a range of practical problems;
3. Translate realistic written and oral
problems into mathematical symbols and vice versa;
4. Draw and attempt to justify conclusions or
hypothesis in relation to sets of data;
5. Make informed decisions based on a
mathematical evaluation of various options;
6. Access the accuracy of results in relation
to a given context;
7. Analyse and interpret data;
8. Discover generalisations and express them
mathematically.
SKILLS
Calculation
Students should be able to:
1. Develop
manipulative and computational skills;
2. Accurately
perform calculations, using a calculator where appropriate;
3. Read
information expressed in mathematical words and symbols;
4. Substitute
in appropriate formulae;
5. Verify
the suitability and reasonableness of a result.
Data
Processing
Students should be able to:
1. Acquire
skills in collecting data from a variety of sources;
2. Develop
skills in organising information
3. Practise
practical methods of summarising and presenting data;
4. Show
facility in drawing graphs and diagrams;
5. Develop
systematic ways of recording information.
Inquiry
Students should be able to:
1.
Develop
investigation and inquiry skills;
2.
Acquire
skills in using multiple references, and reading widely but selectively;
3.
Develop
oral and written communication skills, including the ability to use precise
terminology;
4.
Manipulate
concrete materials, mathematical instruments and measuring devices;
5.
Develop
initiating strategies - seeking patterns, constructing tables, listing.
Thinking
Students should be able to:
1.
Translate
realistic written and oral problems into mathematical symbols and vice versa;
2.
Make
informed decisions based on a mathematical evaluation of various options;
3.
Understand
the nature and role of inductive and deductive reasoning and proof, and reason
inductively and deductively;
4.
Apply
suitable mathematical techniques and problem solving strategies to routine and
non-routine situations.
Communication
Students should be able to:
1. Demonstrate
basic writing skills;
2. Present
work with appropriate setting out and neatness;
3. Clearly
understand instructions and follow them.
Social
Students should be able to:
1.
Accept
responsibility for their own actions;
2.
Follow
directions;
3.
Listen
and be tolerant of others' views;
4.
Contribute
to group discussion and activities;
5.
Start
work without prompting.
6.
Interact
in a cooperative manner with peers and teachers.
Emotional
Students
should be able to:
1.
Develop
self-confidence in handling mathematics;
2.
Persevere
when problems arise;
3.
Develop
a desire to develop their ability
4.
Develop
a positive sense of self-worth
5.
Be
able to make positive use of difficulty and failure
ATTITUDE
TO LEARNING MATHEMATICS
Students should
be able to:
Develop an appreciation of the value of mathematics in society, and
apply this appreciation in their everyday contexts;
Be willing to experiment mathematically in unfamiliar situations;
Show a willingness to participate in the learning of mathematics;
Strive for a neat, orderly and logical presentation;
Positively affirm mathematics as being intellectually exciting.
4.4 values AND CONCEPTS IN MATHEMATICS TOPICS
This section of the
framework extends Section 4.1 Part E.
It is designed to give teachers ideas about how concepts and values
could be identified and communicated in particular mathematics topics. The values are arranged alphabetically in
each topic.
Algebra
Awareness of Consequences:
Indirect link — in equations the value that one
substitutes for “x” results in certain consequences. Indirect link — this
illustrates the influence of cause and effect in life.
Awareness of Potential:
Indirect link — as in asymptotes, we may become
closer and closer to Christ in likeness but never touch Him. Our relationship and potential to grow is
continuous and infinite.
Balance:
Inherent link — solving equations always requires
them to be balanced. An unbalanced or messy sequence ends in the wrong answer.
Indirect link — a satisfying Christian life always
requires a balance.
Caution:
Indirect link — test the solution of an equation to
see if it works. Test things in life to see if they are worthwhile.
Certainty:
Indirect
link — Success or failure are the only two probability options in some aspects
of life
Choice:
Inherent
link — choice is an important part of mathematical reasoning. For example, we
plot lines by choosing values for x and y. We choose between values such as
speed and completing the task in detail or with accuracy.
Indirect
links — many of our choices carry consequences, and we must learn what these
are. The analogy holds for many life situations as well.
Development:
Inherent link — an example is that although the positive
gradient of functions may vary, all are upwards.
Learning from mistakes:
Inherent link — if you make a mistake, try to decide
what went wrong and do not make the same mistake next time.
Order:
Inherent
link — sometimes things need to be re-ordered and sorted out to be useful. Formulae are based on order.
Indirect
link — the transposition of equations is like the Christian life, for in life
we cannot always see the immediate purpose in something.
Positive peer selection:
Indirect link — simplifying by collecting like terms
has a parallel with collecting types of peer friends in life.
Positiveness:
Indirect link — when multiplying negative numbers,
two negatives give a positive. God
turns both positive and negative experiences into positive ones.
Arithmetic
Accuracy:
Inherent link — accuracy implies economy because
when we are accurate wastage is minimized.
We should strive for care and neatness.
Awe:
Indirect link — counting numbers as an infinite set,
as God is an infinite being.
Economy:
Inherent
links — mathematics should encourage efficient use of resources such as time,
effort, space, materials. Economy
includes efficiency in producing results.
Clarity of expression is part of economy. Choosing the most effective
alternative, involves values such as simplicity, conciseness, and clarity.
Informed decision-making
Inherent link — when making choices, the greater the
knowledge, the wiser the decision that can be made. Knowledge is founded on basic skills.
Logic:
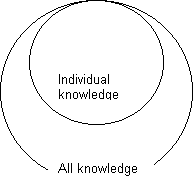
Indirect link — note the venn diagram below on how
knowledge relates to the existence of God:
The diagram shows that knowledge of the
existence of God may exist outside individual knowledge.
Order of numbers:
Inherent link — this can be shown for example in:
magic squares, number patterns, Pascal’s triangle. Numbers and operations are
ordered and wrong answers result if order is wrong.
Place:
Indirect link — in
mathematics, numbers have value according to their place (eg the 7 in 372 is
worth 70). So in life, many things have
value because of their place — place assigns value. We profit from knowing our rightful or appropriate place in many
life situations.
Self-worth:
Indirect link — this can be
shown by place value. For example the value of a digit is determined by its
position in relation to the decimal point. We can let God put the decimal point
in our life.
Calculus
Economy of Resources:
Inherent link — this can be illustrated by using
maximum and minimum values to calculate minimum material needed for maximum
volume etc.
Following instructions:
Inherent
link — following instructions is
being willing to follow set guidelines and rules.
Inquiry:
Inherent link — explores limits, and considers the
infinite and the finite.
Logic in Reasoning:
Inherent links — deductive and inductive reasoning
are based on logic.
The
results of logic are only as dependable as the truth of the original premise.
Two
types of reasoning are deductive and inductive:
Mind Expansion:
Inherent link — calculus can be a tool available to
attempt problems not solved by previous knowledge.
Positive Use of Difficulty
and Failure:
Indirect link — an example of this trait is as
follows. The turning point in a graph
occurs when f1(x) = 0, so often the turning point in life occurs when
we reach our lowest point.
Reference To Principles:
Inherent link — Reference to principles is our
derivation of why we do what we do. In calculus we use first principles to
explain why we follow a set method, then we just keep using that method knowing
in the back of the mind why.
Indirect link — even though we do not always think
every action through every time we act, we need to be aware of the basic
original reason for doing what we do.
Consumer
Arithmetic
Arranging
Priorities:
Inherent link — money is not everything. We should be able to put money into its true
perspective.
Economy:
Inherent link — economy refers to the ability to
calculate values for wise spending and investing.
Responsibility:
Inherent link — responsibility refers to living
within your means.
Sharing:
Inherent
link — we should develop the concept of planning to be able to help other
people. We should not keep everything
to ourselves.
Stewardship:
Inherent link — is budgeting, and responsible usage
of funds (credit cards etc). The
mathematics of consumerism often stresses the importance of stewardship when
making decisions about purchasing goods.
For example, students can be shown the importance of comparing prices
and looking for the best buy.
Verification:
Inherent link — Verification is the ability to put
something to the test, and to check its real value.
Wise Choice:
Inherent link — wise choice is the ability to make
informed intelligent decisions about spending.
Worth:
Inherent link — worth demonstrates the value of
mathematics in its practical application to living, hence its practical value.
Mathematics helps us to live as a more useful citizen in our society.
Geometry
Acceptance of Paradox:
Indirect link — a point is not really a point but a
representation of a point. This concept is still very useful and important, and
parallels our incomplete understanding of God.
Appreciation of a Designer:
Indirect link — in engineering the strongest shape
is a circle — like the trunk of the tree.
The tree, designed by God is everywhere in nature.
Design economy:
Inherent link — the mathematics of the honeycomb
shows the economy of design. Economy
produces the greatest strength and volume from the smallest amount of material.
Logic:
Indirect link — by deductive reasoning and through
observation of the world we can deduce a creator’s
hand.
Reasoning Process:
Indirect link — design in nature (logarithmic spiral
of nautilus shell or honeycomb) can be used to support the argument for the
existence of a Designer.
Utility of Pattern:
Inherent link
— the usefulness of pattern is illustrated as follows:
Mathematics
expresses the concept of pattern in nature.
There
is a high degree of dependability of pattern in nature.
Pattern
is a tool for observation, and a tool for analysis.
Pattern
is a means for prediction.
Geometrical
patterns are the building blocks for both technology and beauty.
Number
patterns are the basis of mathematical theories.
Pattern
in statistics enables prediction and forecast with a high level of dependability.
Probability
is sometimes observation of pattern.
Measurement
Accuracy:
Inherent links — accuracy is something we should
always strive for. The limits to
accuracy of results are dependent on the limits of the original
measurements. We must recognize types
of errors. Two types are: avoidable which include systematic errors
such as parallel, transcription errors; and unavoidable which depend on factors such as the level of
accuracy of measuring instruments. We
may strive for accuracy, but we should recognize its limits.
Choice:
Inherent link — choice is using correct and
reasonable units of measurement, and a suitable level of accuracy for different
situations.
Disciplined Memory:
Inherent link — formulae must be learned. It takes effort to learn some things.
Economy
Inherent link — economy is being able to calculate
requirements that are needed, and to save wastage.
Finding God
Indirect link — as with measurement where we do not
need one hundred percent accuracy for it to work, we do not need to understand
everything about God for Him to work for us.
Open mindedness
Inherent link — we should not take the first or most
obvious measurement for granted, but we should consider other possibilities
before starting our problem solving.
Practicality:
Inherent link — there is a practical use in
measurement, yet there is not one hundred percent certainty or accuracy. Measurement is not absolute, but is only
accurate to a certain point.
Verification
Inherent link — verification is being able to
measure for yourself, to double check and save being “ripped off.”
Worth — Practical
Inherent link — measurement can demonstrate a
practical application of math’s, and shows that math’s has practical value.
Probability
Logic:
Inherent link — give gradations in examples of
probability such as one in ten, one in fifty, one in a hundred, one in four
million, and mention the probability of winning something like Tatts Lotto.
Indirect link — As an example of probability, there
are too many factors and combinations of factors to make evolution
probable.
Perceptiveness:
Inherent link — independent events do not
necessarily affect each other. Superstitious people believe events are
connected when they really are not. Psychological and supernatural factors can
alter this relationship.
Personal responsibility:
Inherent link — probability says there is only
likelihood, not a certainty. An example is death by cancer. Probability does
not control or determine actual outcomes. It concerns groups not individuals. The larger the group, the more likelihood of
the laws of probability operating.
People get a false sense of security with probability. An example is when they consider car
accidents or death by lung cancer.
Personal responsibility:
Indirect link — emphasize that life is not random,
so personal responsibility is needed to make the world better.
Progressiveness:
Indirect link — it is possible to escape from
probability. An example of an escape is some person who has made a
socioeconomic escape through personal development to escape probability.
Stewardship:
Inherent link — explain why gambling is not
productive — there is a gap between initiative and mathematical probability.
There is need for careful spending on insurance which is based on probability. For example a non-drinker, non-smoker has
cheaper insurance in companies such as ANSVAR.
House insurance premiums are determined by location according to crime
areas.
Wise choice:
Indirect link — wise choice affects the outcome,
whether this is mathematical or related to life. With salvation there are two
outcomes — saved or not saved.
Emphasize that by choice you can increase the probability of something
happening.
Problem Solving Ability
The skill of problem solving is related to many
mathematical values. Examples include
the following:
Acceptance of value tension:
Inherent link — when solving problems, we have to
keep in mind competing values. Examples
are speed of operation versus task completion.
Anticipation:
Inherent link — to find minimum and maximum values
when solving some problems, foresight is required. Anticipation pays dividends.
Awareness of parameters:
Inherent link — problem solutions often fall into
certain parameters (for example time and cost). All the parameters have to be
kept in mind constantly.
Indirect link — when making decisions in life, it is
also necessary to juggle parameters.
Care in technique:
Inherent link — when solving problems, the technique
is often as important as the answer. It
can be important to carefully record the way we solve problems for future
reference.
Careful problem formulation:
Inherent link — problems in mathematics often occur
simply because of the way the examples are formulated.
Indirect link — the same holds for life’s problems.
The way we state or see something can itself be the problem.
Creativity:
Inherent link — we use different approaches to solve
problems. We develop different
"proofs" for mathematical theorems.
Order:
Inherent link — algorithms have a basis in order.
Sequence and Series
Acceptance of Paradox:
Indirect link — there are paradoxes in design. So in life apparent contradictions can be
working together in a large scheme.
Aesthetic appeal :
Inherent link — golden ratios are pleasing to the
eye.
Dependability:
Inherent link — the value of dependability is shown
in a sequence.
Economy of design:
Indirect link — Fibonacci Series occurs often in
nature eg. 1, 1, 2, 3, 5, 8 etc, suggesting an intelligent source for number
patterns:
found in pine cones, sunflower, pineapples.
it also indicates one source and mind rather than mere matter.
relates to Pascal’s triangle, again reinforces the same thread of there
being a pattern or design. this indicates economy of design.
Flexibility:
Inherent link — in sequences certain steps need
not be reversed, while others must be able to be reversed. For example, the statement “if and only if”
is one that is true as it reads, and also in reverse.
Indirect link — In life, some things are
reversible, but some are not. We need
to know the difference.
Order:
Inherent
link — sequences and series are orderly. Mathematics is a system that reflects
order. Mathematical modeling works on the assumption that nature is orderly.
Predictability:
Inherent link — predictability comes from working
out formulae from patterns. This process relates to making intelligent choices.
Indirect link —
predictability can be a support for design and a designer.
Trigonometry
Awe:
Indirect link — Awe is a sense of wonder through a
look at the infinite. We can use tan graphs to help achieve awe.
Care:
Inherent link — care is diligence in assessing,
interpreting and analysing the information given to start with.
Choice:
Inherent link — choice is selecting the correct
ratio in the process of obtaining a correct result.
Courage:
Indirect link — courage means willingness to
experiment, to make a start even if you cannot
see the end from the beginning.
Disposition to search:
Inherent link — there is no end to knowledge. For
example, after angle sum and pythagoras, there is still more.
Investigation:
Inherent links — investigation is discovering
real-life uses of trigonometry. Examples are navigation, astronomy, and
surveying.
Logic and Order:
Inherent link — logic and order refer to making sure
that statements follow the correct pattern, and that they are true.
Pattern:
Inherent
link — pattern shows us how the trigonometry graphs in life vary in occurrence
(light, sound, heartbeat, pulse rate etc).
4.5
attitudes TO CLASSWORK
Listed below are some classroom attitudes necessary
for students to develop if they are to grow in their mathematical ability and
ability to cope with life. Each attitude is stated in the context of what
teachers may do to encourage its development.
Courage:
·
Encourage
students to face mistakes, to give answers in front of class when unsure, to
ask questions or ask for help, to persistence, and to have the courage to
question teacher or book answers.
Enjoyment:
·
Foster
enjoyment through success. The teacher’s approach should ensure that success
happens so enjoyment follows. Provide a pleasantly decorated room.
Honesty:
·
Educate
students to use answers wisely as learning experiences.
·
Ensure
students refrain from copying from others.
Learn from
mistakes:
·
Help
students realise that all people make mistakes, including text book writers,
and that mistakes show students’ weaknesses and strengths in topics.
·
For
brighter students, point out that mistakes show carelessness. Text corrections are very important.
Mutual
cooperation:
·
Arrange
activities so more able students can help others.
·
Provide
opportunities to show cooperation in student-teacher relationships.
Neatness:
·
In the
course of teaching, emphasise attention to detail, taking time with diagrams,
clearly defining answers, accuracy in use of symbols and signs, no liquid
paper, crossing out with a single line.
Organisation:
·
Ensure
students learn organisation in their arrangement of folders, notes, tests,
corrections, and use of time.
·
Discourage
wasting time with undue embellishments such as changing colours in assignments.
Respect for
self and others:
·
Keep
emphasising that every one has ability and is able to contribute in some way,
and can be considered useful.
·
Insist on
tolerance for those who differ in race, religion, ability, beliefs, ideas, and
ways of doing things. Do not allow students to laugh at the mistakes of others.
·
Disapprove
of derogatory statements about lower mathematics levels and those of lower
ability.
Self-confidence:
·
To build
confidence, have students experience success at the beginning of unit in
particular.
·
Emphasize
that making a mistake does not mean failure.
·
Attempt
problem solving in varying circumstances.
·
Attitude of
teachers to students must be positive. Avoid put downs.
·
Lower
ability students can achieve in certain areas.
Provide opportunities for them to do so. An example of a good topic is
tessellation’s.
Self-discipline:
·
Encourage
students to do homework because of personal benefits, doing as much as they can
rather than as little as they can. Show
the wise use of answers, and benefits of making personal sacrifices, and
patience. Emphasize patience, particularly if success is delayed.
Sense of
justice:
·
To develop
a sense of justice, fairness must be seen in discipline and marking;
·
Teachers need
to admit a mistake and apologise if necessary.
Time:
·
Emphasize
efficiency of time, and quality of time. There needs to be short periods of
concentrated effort, and undisturbed time.
·
Return
tests and assignments in reasonable time
·
Allow
planned study and revision time.
·
Be an
example of punctuality, showing the need to be on time
·
Ensure
students hand in assignments on time.
·
Finish
class on time.
Trustworthiness:
·
There is
value in teacher expectations being met. For example give enough responsibility
for students to work well when left alone. Students can mark their own work at
times. Homework should be done for the benefits gained, rather than through
fear of detention.
Assessment is the
measurement of students' performance in relation to the outcomes of their
courses.
Assessment can take many
forms. Informal assessment is carried
out through questioning and observing individual students as they work, while
examinations and tests are examples of more formal means of assessment.
The assessment should assess
a range of outcomes which include knowledge, attitudes and skills, and not just
recall. A range of assessment methods
is needed to assess this range of learning abilities.
Assessment may be carried
out for one or more of the following reasons:
·
To find
what existing knowledge or prior experience students bring to the learning
task;
·
To monitor
the progress of students;
·
To provide
motivation;
·
To provide
feedback to students;
·
To measure
the extent to which students meet the course objectives;
·
To
establish a single global mark;
·
To assess
students’ potential in the subject;
·
To provide
feedback to the teacher.
Assessing Values and Attitudes
Assessment should take account of the learning of
values and attitudes. Values are
estimates of worth placed on some aspect of experience. Attitudes can be seen as values revealed in
action in the longer-term. They may be
dispositions to behave in certain ways because of values held, or a group of a
person’s beliefs organised around situations, people or objects, and held over
time. The assessment of values and
attitudes can be difficult to put marks to, but certain kinds of such
assessment can be done.
Values
·
Have
students identify values or recall values taught. Assessment of awareness of values can occur in tests and
assignments. Seven categories of values
are mentioned in this framework.
·
Have
students make value judgments or choices about mathematical procedures. These judgments and choices can be assessed
on the quality and types of evidence or criteria used.
·
Have
students make their own links between mathematical concepts and life
experience, whether this experience is purely intellectual or more
spiritual. The criterion of creativity
could be applied to this process.
Attitudes
Students need to be aware of desirable attitudes
about mathematics, and know why these are important. It is important to look for changes in attitudes over time.
Assessment of attitudes can be based on observation of students in the
longer-term, not just on isolated incidents. Observation can be done by:
·
Teacher
assessment and recording of comments.
·
Self-assessment. Here students assess themselves. Students can be surprisingly honest and
perceptive about their own attitudes.
·
Questionnaires. Student attitudes can be assessed by
completion of questionnaires.
Reporting on
attitudes and values
Marks: The valuing process and attitudes could be given a weighting when
compiling the overall course mark (for example ten percent or less). This could be part of test marks or
continuous assessment.
Profiles: A listing of desired values and attitudes could be made and then
either:
Indicate on a check list those which are observed
(based on reflection or impressions over the term, or accumulated in check
lists);
Or report only those observed (based on reflection
or impressions over the term, or accumulated check lists). In this way teachers can build a description
of a set of values and attitudes students hold about mathematics and learning.
Rating scales. Use a four or five point rating scale.
Descriptive
statements. Assessments can be referred to when
completing reports or testimonials which describe students’ attitudes more
subjectively.
It is clear that students
achieve better when learning expectations are spelled out clearly and
regularly, when assignments are well structured, and when assessment results
are provided promptly. This fact is
particularly important in relation to the valuing part of learning.
Evaluation
Evaluation extends beyond
assessment of how well students are reaching objectives. It goes further in attempting to judge the
merit of the course and its objectives, and it seeks ways to constantly improve
instruction. Therefore some evaluation
could be informal. Teachers may for
example observe classroom signs of teaching success, interview students
informally about the course, or ask them to evaluate the course in a written
questionnaire. Good teachers enjoy
their success, but keep a critical eye on their own performance.
SECTION 5
Appendices
5.1 What are Values? . . . . . . . 42
5.2 A Christian Approach to
Values . . . . 42
· A
Marriage of Mathematical and Christian Worldviews . 43
· The
Debate About Reality – An Historical Sketch . 43
5.1 What Are Values?
Values
are core beliefs or desires that guide or motivate attitudes and actions. They also define the things we value and
prize the most, and, therefore, provide the basis for ranking the things we
want in a way that elevates some values over others. Thus, they determine how we will behave in certain situations.
Values
can be classified under a number of headings such as aesthetic, application to
life, creativity, emotional, intellectual, social, spiritual. Examples of each are given in Section 4.1
previously.
Values
can also be classified as nonethical or ethical.
Nonethical Values
Much
of what we value is concerned with things we like, desire, or find personally
important. Wealth, status, happiness,
fulfillment, pleasure, personal freedom, being liked and being respected fall
into this category. They are called
nonethical values since they are not concerned with how a moral person should
behave, for they are ethically neutral.
Ethical Values
Values
become ethical when they directly relate to beliefs concerning what is right
and wrong (as opposed to what is correct, effective or desirable). Ethical values are established by moral
duties or moral virtues. Moral duties,
such as honesty, fairness and accountability, oblige people to act in certain
ways according to their moral principles.
Moral virtues go beyond moral duties.
They refer to moral excellence, characteristics or conduct (for virtues
include characteristics such as charity, temperance, humbleness and compassion.
5.2 A Christian
Approach to Values
Christian Worldview
There
has been a trend amongst educators recently for programs to be ethically
neutral and not favour any particular religious or philosophical point of
view. The outcome has been that
students, regardless of their social, racial, and economic background, have
absorbed the unmistakable message that right and wrong are relative, that there
are no core ethical moral precepts, that they must not be judgmental, that what
is right for one person maybe wrong for another. Thus right and wrong are regarded as personal values, never
universal or absolute and always dependent upon time, place and circumstance.
A
christian world view, however,
·
Accepts the
values position that such precepts as stealing, cheating and lying, for
example, are wrong
·
Assumes the
biblical principal that people are innately sinful and, when left entirely to
their own devices, do not always choose the rational and good
·
Assumes the
existence of a certain set of core value principles that are based on Christian
teachings as are expressed in the Bible
·
Uses the
core set of values in order to examine particular situations and choose
behaviour accordingly
·
Adopts the
principle that values, whether nonethical or ethical, only have ultimate
meaning in a biblical perspective
·
Emphasises
the principle and ethical values because it focuses on God as the source of
reality, which included perspective
Values
are derived from the worldview that sees some form of quality as being the
primary reality of human existence.
Values are estimates of worth or quality in some aspect of human
experience. These qualities include
moral goodness and all other aspects of goodness and quality believed in by the
ancient civilisations before that later Greeks.
5.3 A Christian Approach to
Teaching Mathematics
A Marriage of Mathematical
and Christian Worldviews
A worldview can be described as “a framework or set
of fundamental beliefs through which we view the world and our calling and
future in it” (Olthius, 1985)
The traditional mathematical worldview sees reason
as being the chief source of our beliefs.
Probability is not enough basis for belief, so the deductive method or
reasoning is adopted. The starting
point of reason is certain, so all that follows should also be certain.
Christians see nothing wrong with the use of reason
in mathematics or anywhere else.
However they do have a problem with the notion of “reason alone” as the
sole source and justification of their beliefs.
The Christian worldview is based on an appeal to authority. Through faith it sees God as the source of
everything. His knowledge is
communicated in the Scriptures that are certain and wholly true. The goodness of God is important in this
view because this guarantees he will not intentionally mislead people. By contrast human knowledge is probable and
fallible because such knowledge is biased.
Therefore Christians would rather surrender their belief in 1 + 1 = 2
than belief in God and his love.
The
task of the Christian teacher is to integrate these two views, as is
illustrated by the venn diagram below.
Bibliography:
James Olthuis, On World Views, Christian Scholars Review, xiv, 2, 1985, p.155.
The Debate About Reality —
An Historical Sketch
Worldviews attempt to state what is real. Ancient
worldviews such as those of the Hebrews, the early Greeks and many Eastern
nations accepted that the idea of “God” or some form of “goodness was the great
reality of life. These words in the ancient languages also had the same
linguistic roots as other words such as “oneness,” “virtue,” “excellence” and
“quality”. These ideas were seen to best reflect what was real, and generated
the mythos — the collection of
stories that comprised human cultures.
The later Greeks attacked this worldview in two
ways. In their search for a “universal principle” as an expression of oneness
in nature, the cosmologists ended up splitting the oneness of “God” and
“goodness” into two parts — form and substance, subjects and objects, mind and
matter etc. This paved the way for a later debate about whether truth was more
important than goodness. In this debate Plato and Aristotle relegated the idea
of goodness to being less important than truth as the best pathway to find
reality.
The ongoing debate about truth being more important than goodness has
set up a potential conflict between the worldviews of mathematics and
Christianity. This framework wishes to resolve this conflict, believing that
mathematics is more than reason because it reveals some of the “quality” found
in God. The truth that mathematics seeks is not necessarily opposed to this
quality, but is rather part of it.